The Orbital Debris Collision Hazard for
Satellites in Geostationary Orbit
Duncan Steel
2015 April 29
Introduction
In my two previous posts (here, and here) regarding the orbital debris collision hazard I have been considering only test satellites in low-Earth orbit (LEO). In this post I turn my attention to satellites in geostationary orbit (GEO); that is, satellites in orbits that have periods of one sidereal day (i.e. altitudes near 35,800 km) and are in near-circular (i.e. low eccentricity) paths close to the equatorial plane (i.e. low inclination). Such orbits are used for many communications satellites, and are sometimes termed Clarke orbits.
A crude estimation of the typical collision probability in GEO
In principle it is straightforward to derive an estimate of the collision probability with space debris for a satellite in GEO. Consider the diagram below. The white circle shows the orbit of a geostationary communications satellite: there are many such satellites in GEO, but they remain in set positions due to their operators performing station-keeping burns/manoeuvres and so cannot collide with each other. Even a GEO satellite which is no longer under control only has a small drift speed (much smaller than the GEO orbital speed of 3.075 km/sec) and so the risk of inter-satellite collisions is very small, if we are considering only true geostationary satellites.
This is not true, however, for orbiting objects that cross the GEO altitude. The red ellipse in the diagram is intended to represent a rocket body in a geostationary/geosynchronous transfer orbit, having performed its purpose in carrying a GEO satellite to the necessary altitude. That defunct rocket body will pose a collision hazard to all functioning satellites in the geostationary band, as its argument of perigee and longitude of the node precess under gravitational perturbations due to the Moon and the Sun, and also the Earth’s oblateness (dependent upon the altitude of its perigee).
Imagine a sphere with radius (r) equal to the distance of the geostationary band from the centre of the Earth (about 42,000 km). That sphere has an area of 4πr2. The rocket body, having an apogee above the geostationary band as shown, crosses that band twice per orbit, giving it two chances to hit that one particular communications satellite. If we estimate the mutual collision cross-section to be 100 square metres, then the probability of a collision is given by 2 × 100 / 4πr2 which is a shade less than one part in 1014 per orbit of the GTO object (the rocket body). That GTO will have a period lower than one sidereal day, perhaps about 15 hours, or one part in 584 of a year, so that our estimate of the mutual collision probability becomes about 5 or 6 × 10-12 per year.
To put that figure into some perspective, the universe is about 13.8 billion years old, and so a mutual collision would have a probability of occurrence of less than ten per cent over such a timescale. (Of course, the solar system is only about one-third the age of the universe; and over such phenomenal timescales all manner of other things happen.)
This, however, was a calculation for a mutual collision between only one pair of orbiting objects. The reality is that there are hundreds of satellites in geostationary orbit; and hundreds of rocket bodies and fuel tanks and other debris items crossing the GEO altitude, so that a more sophisticated assessment of the collision hazard is warranted.
Specific example orbits
The Inmarsat 5F2 communications satellite was launched on 2015 February 01 and inserted into geostationary orbit. The Briz-M rocket booster that was used to carry it to its final altitude remains in a GTO similar to that shown in the preceding diagram. Orbital parameters for the two objects in question are shown in the table below; note that the inclination and eccentricity of Inmarsat-5F2 in particular will vary from day-to-day and week-to-week under the influence of gravitational (and radiation-induced) perturbations, plus station-keeping burns by the operating company.
| Name | International Designator | Satellite Catalogue Number (SCN) | Perigee altitude (km) | Apogee altitude (km) | Eccentricity | Inclination to the Equator (degrees) |
| Inmarsat-5F2 | 2015-005A | 40384 | 35,551 | 36,029 | 0.000165 | 0.0338 |
| Inmarsat-5F2 Rocket Body | 2015-005B | 40385 | 2,775 | 63,223 | 0.767648 | 27.6213 |
| Inmarsat-5F2 Fuel Tank | 2015-005C | 40386 | 355 | 14,849 | 0.518453 | 50.7385 |
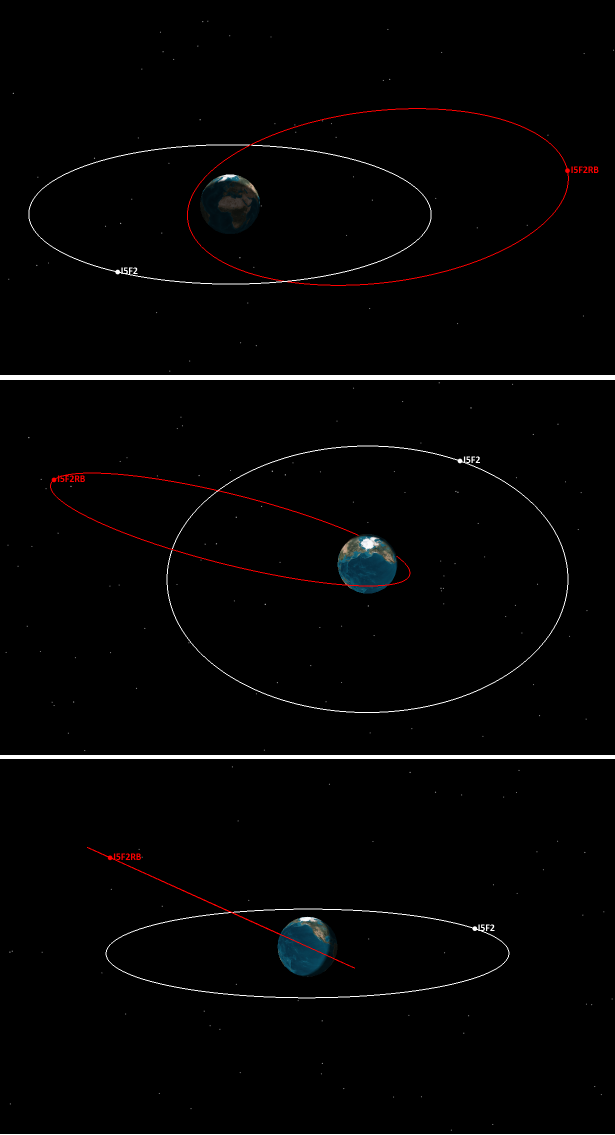
The final line in the table, for the fuel tank left in a lower orbit, plays no further part in the present calculations and is included simply for completeness. The orbits of the first two objects are shown in the graphic below, with three views being given so as to indicate the three-dimensional nature of the geometry. In addition a short movie portraying the movements of the two objects over five days is available for viewing and download from here (1.44MB).
Graphic above: The orbits of the Inmarsat-5F2 satellite (in a near-circular geostationary orbit) and also the rocket body that carried it there, that rocket body (labelled I5F2RB above) having been left in an orbit with eccentricity near 0.77 and a perigee altitude of a few thousand kilometres.
Using the orbital parameters listed above I can now calculate the separate collision probabilities involving (a) Inmarsat-5F2 itself; and (b) the Briz-M rocket body used to carry Inmarsat-5F2 to its geostationary orbit, against all objects in the tracked orbiting object catalogue. In a previous post I described the list of 16,167 tracked items that I have been using in calculating collision probabilities. Again using that list I have derived the following results:
| Object | Number of tracked objects crossed by the I5F2 objects | Net collision probability per square metre per year |
| Inmarsat-5F2 | 1,543 | 3.06 × 10-8 |
| Inmarsat-5F2 R/B | 3,763 | 1.15 × 10-9 |
Discussion
The collision probabilities derived above are in units of per square metre per year, and are based on a model test satellite in each case having a spherical shape and a geometrical cross-section (and therefore collision cross-section) of one square metre. Of course, the actual objects in question do not have such a size and shape.
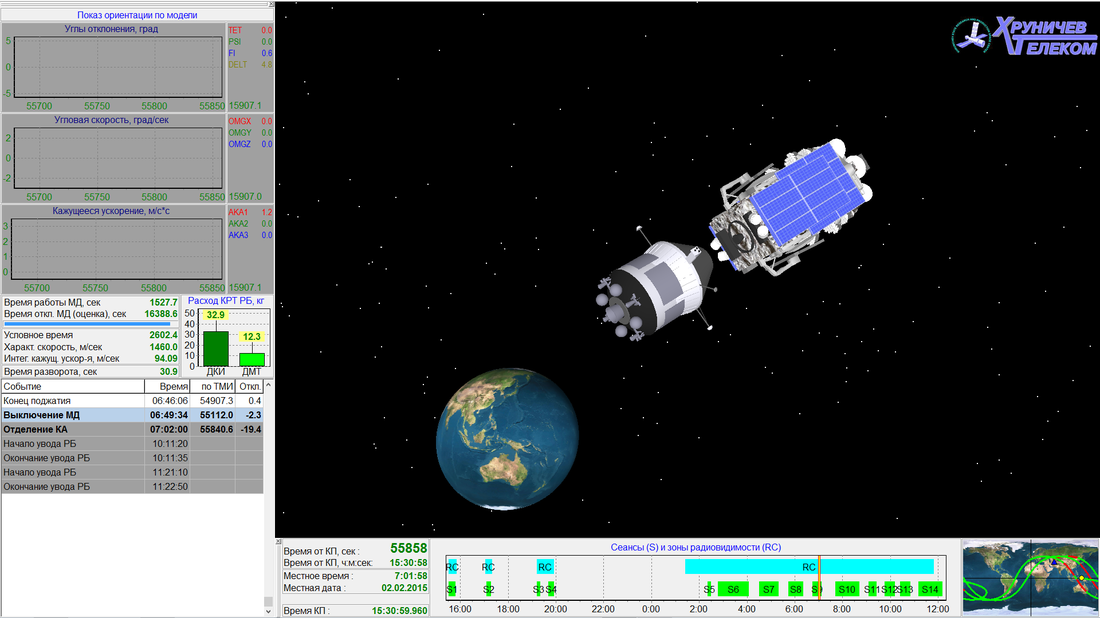
The two are shown in the graphic below (the source of which is here). The Briz-M booster might be modelled as being near-enough to spherical for present purposes, with a characteristic size (diameter) of almost five metres, and so a cross-sectional area of about 20 square metres.
Graphic showing the Inmarsat-5F2 communications satellite (upper right) and the Briz-M rocket booster (centre). Courtesy Khrunichev.
The Inmarsat-5F2 satellite is much larger. Once its solar cells were deployed it attained a greatest linear dimension of 33.8 metres, and the thermal radiators and antennas that fold out from the main bus render linear dimensions of 8.08 metres. Looking at the satellite from orthogonal views its greatest cross-sectional area is therefore about 270 square metres, and its smallest about 65 square metres.
During its orbit around the Earth the satellite rotates its solar cells so as to keep these pointing towards the Sun, and the effect of this is to ‘average out’ the cross-section from the perspective of potential colliders such that again we might approximate its collision cross-section in terms of a sphere with a cross-sectional area of about 150 square metres, as a rough estimate.
Using that as a collision cross-section one derives a collision probability for the Inmarsat-5F2 satellite of about 5 × 10-6 per year (i.e. 150 × 3.06 × 10-8) and so a characteristic event rate of one collision per 200,000 years.
This value, however, is misleading: as noted earlier, most objects in the geostationary belt are moving in step, making it infeasible for them to collide with each other. One approach I could take here would be to sort through the 1,543 objects crossing the orbit of Inmarsat-5F2 and weed out those that are also truly geostationary or geosynchronous, making collisions with each other impossible in the present epoch, but it is sufficient to say simply that the true collision probability against other tracked objects is likely an order of magnitude less than the value calculated here (and so around 5 × 10-7 per year, or a timescale of two million years).
Turning to the Briz-M rocket body, there is nothing to protect it from collisions with objects in the geostationary belt (or anywhere else). The collision probability for this object is therefore about 2.3 × 10-8 per year (i.e. 20 × 1.15 × 10-9) and the characteristic collision time is of order 40 million years.
In my first post here on orbital debris I discussed three different ways in which the ‘true’ collision probability could and would be higher than my calculations indicate, these ways being:
(i) The Satellite Situation Report and Two-Line Elements that are publicly-available do not include any CLASSIFIED orbits, these comprising almost 800 objects compared to the 16,167 in my listing used in these calculations;
(ii) Many of the tracked objects are larger than my model spherical satellite of cross-sectional area one square metre, so that the true collision cross-section for specific cases will be substantially larger than one square metre; and
(iii) The tracked objects are larger than about 10 cm in size, else they are not detectable with the ground-based optical and radar sensors employed by the U.S. military to keep tabs on anthropogenic orbiting objects, but fragmentation events such as remnant fuel explosions and hypervelocity collisions will produce many orbiting objects smaller than that 10 cm limit.
Taking each of these considerations in turn:
(i) There are certainly various CLASSIFIED payloads in geostationary orbit, and rocket bodies used to take them there also have GEO-crossing paths, but the effect of including these is unlikely to boost the derived net collision probability for objects in geostationary orbit by more than 50 per cent;
(ii) The communications satellites in GEO tend to be the largest objects in such orbits (unlike in LEO, where the International Space Station, the Hubble Space Telescope and various classified surveillance platforms dwarf most other satellites) so that the appropriate collision cross-sections to use are indeed the sizes of the communications satellites themselves, with areas dominated by solar cell arrays and typically being 100-300 square metres; and
(iii) There is very little small debris in orbits crossing the geostationary band, and so the enhancement in the collision probability due to sub-decimetre projectiles is small.
Overall my analysis leads to an expectation that the individual lifetimes of satellites in the geostationary band against catastrophic collisions with artificial space debris are of order millions to tens of millions of years.
Conclusions
I will now repeat what I have just written: the individual lifetimes of satellites in the geostationary band against catastrophic collisions with artificial space debris are of order millions to tens of millions of years.
If this conclusion is correct then, from the perspective of satellite protection and safety, there is no real need to boost defunct satellites into higher orbits, as is current practice. Indeed one might argue that to do so may have the effect of increasing the collision hazard: in any orbital manoeuvre there is a finite likelihood of something going wrong, perhaps with disastrous consequences. For example, re-igniting a rocket booster attached to a communications satellite, when that booster had been dormant for a decade or more since the satellite was placed in its desired station, might lead to an explosion and thus the spreading of myriad pieces of debris around the geostationary belt with high relative velocities. It would be better to leave the satellite as it was, simply closing it down until future generations with better technical capabilities can clear it up.
If the debris impact timescale for geostationary orbits is indeed of order millions of years, the collisional impact risk for satellites in that high-altitude band is dominated by the flux of natural meteoroids. I will say nothing more on that subject here, and simply refer the reader to a recent report on the subject.