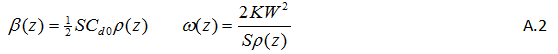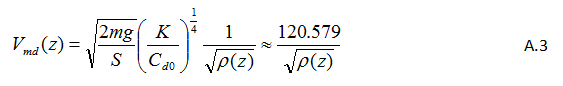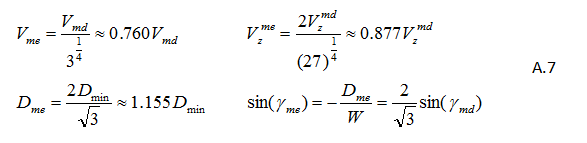Optimal Gliding Descent Scenarios for MH370

Geoff Hyman, Barry Martin and Sid Bennett
14 July 2015
(Updated 15 July 2015)

 

Introduction

In this note we focus on the final descent of the flight of MH370 and explore the implications of an assumption that the last stage thereof was executed in the form of a glide rather than a spiral descent.

Glide scenarios are of interest because they may assist in the identification of an outer boundary of the search area. Whether MH370 descended in the proposed manner is not resolved here. On the other hand, lack of success in terms of finding the aircraft within the current priority area further raises the interest in plausible alternatives.

On best-available interpretations of the available satellite and flight simulator evidence, optimal glide scenarios represent extreme cases and would not be considered to be the most likely ones to have actually occurred. However, as long as glide scenarios, in some form, are a reasonable possibility, the implications for the search area merit further consideration.

This study was motivated by a proposal that, if under (human) pilot control, MH370 could have continued on an efficient gliding path after passing the 7th arc (00:19:29 UTC; all times herein are UTC). Previously [1] we explored an apparent anomaly in the BTO/BFO observations associated with the re-log-on event at 18:25 and SATCOM handshake transmissions shortly afterwards, concluding that an offset track might have been the cause. Such scenarios would have required human input after the time of final primary radar contact. Combining such considerations with the analysis reported in [2] provides a motivation for the scenarios examined here.

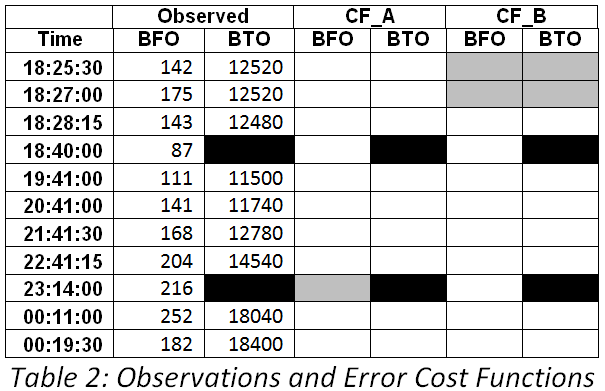
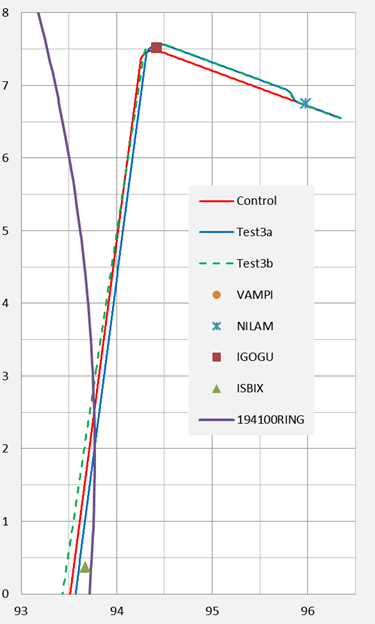
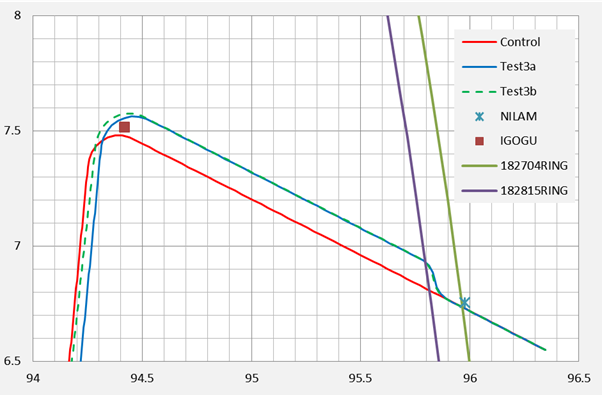
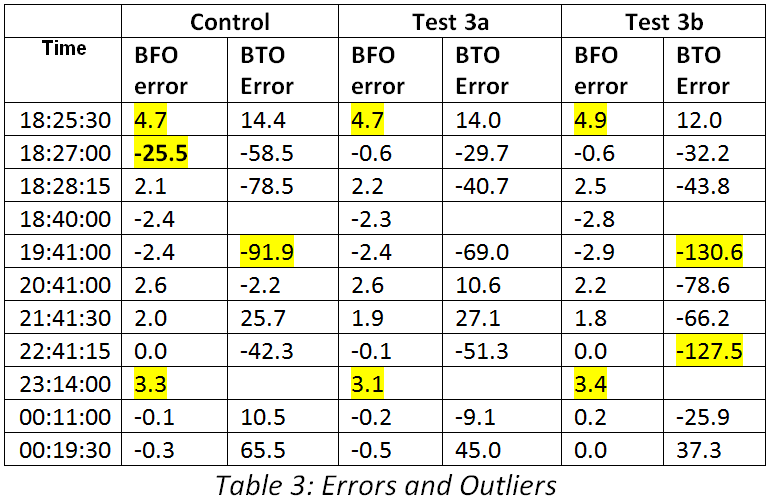
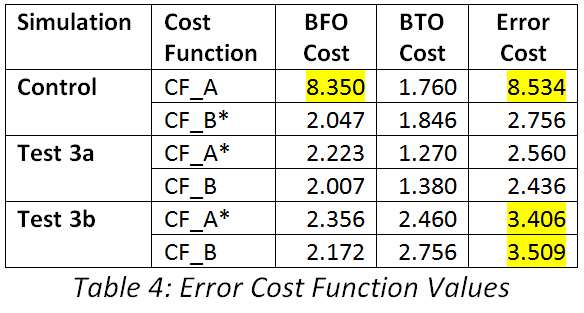
The present study considers a scenario involving events subsequent to 00:11, but there are only two satellite observation pairs available: at 00:11 and at 00:19:29. Inmarsat engineers [3] are confident that the corrected 00:19:29 BTO is usable. The assessment of alternative flight paths after 00:19:36 is problematic because no further BFO or BTO values were recorded. The current simulations are computed in 15 second time increments and are divided into two parts: the first is for the period with satellite observations, from shortly before 00:11 until 00:19:30; and, the second is an extrapolation of the position at 00:19:30 to the end of the flight.

The likelihood of MH370 having executed a simple glide descent, resulting in the aeroplane being ditched at considerable distance from the 7th arc,  is conditional upon rejecting the validity of the BFO at 00:19:29 as it is presently understood [3].  The BFO measurement is a part of the handshake during a re-log-on event with the Inmarsat ground station at Perth and we do not have sufficient comparative data to determine whether the BFO anomaly referred to by Inmarsat for the log-on sequence at 18:25 should be considered in this circumstance as well.  Further data from the ATSB relating to the log-on events would be welcome, including comparable data from similar flights. If the BFO measurement during the re-log-on (at 00:19:29 ) were to be determined to be valid, then the descent scenarios could be complex, and less efficient, with shorter ranges and/or reduced times aloft.

One consideration was the conflicting initial assessment of the location of the intersection of the flight path with the 7th arc. Subsequently, our group has reported a number of studies that strongly suggest that the location of that intersection is quite well established. This intersection may be some appreciable distance from the final location. However, with due recognition of the uncertainty of the descent trajectory, this still facilitates a more focused review of the future search area.

The current report also incorporates improvements to wind modelling, informed by [4]. It also includes refinements to deal with the brief period for which only one engine was operating.

 

Optimal Glide Scenarios

We consider two possible types of optimal glide scenario: maximum range and maximum endurance. The associated altitude profiles for speed and descent speeds are based in the relationships given in annex A below. These profiles are based on a drag model for the airframe alone which does not account for drag contributed by windmilling powerplants.

For the one engine inoperative (OEI) case the single engine thrust also needs to be incorporated. However this only applies to a brief period of the descent and is not reported here.

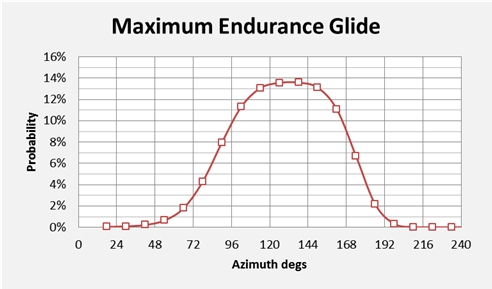
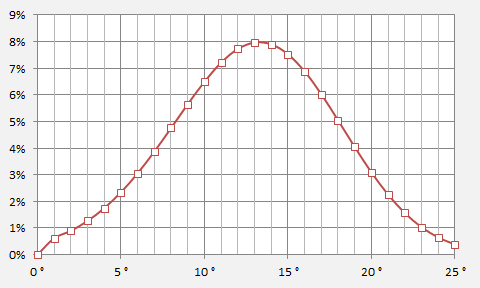
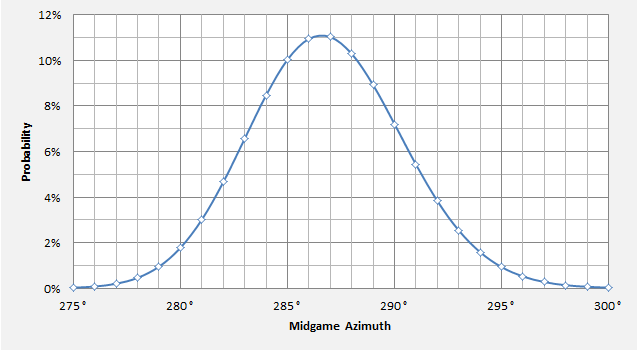
In Figure 1 we show a distribution of likely flight directions at the commencement of the glide stage. For the maximum range scenarios there are two modes (or peaks), while maximum endurance scenarios show a single peak.

Our previous studies indicated that the most likely flight azimuth, prior to the 6th arc, was 186 degrees True (i.e. six degrees to the west of due south). It appears that, after the second engine flame out, the aeroplane probably made a turn to the left through an angle of at least 20 degrees; alternatively our speed assumptions during the loss-of-power event might be too low. For both sets of glide scenarios the median azimuths are similar, the main differences being their implications for the distances flown beyond the 7th arc.

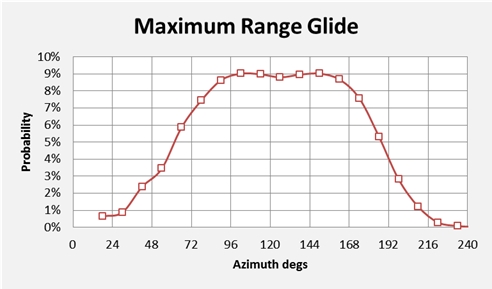
Figure 1: Initial direction for the Glide: a) Best Range; b) Best Endurance.

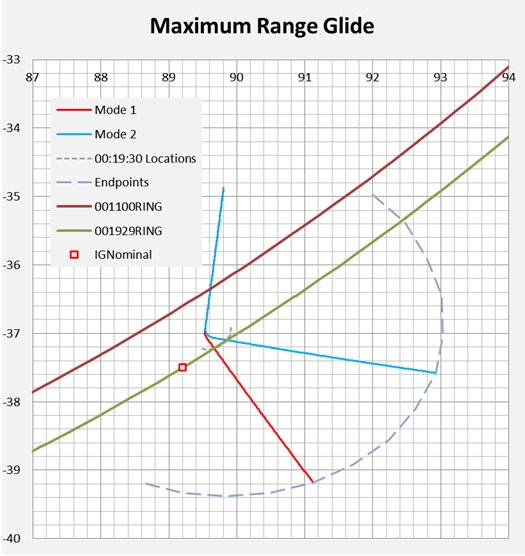
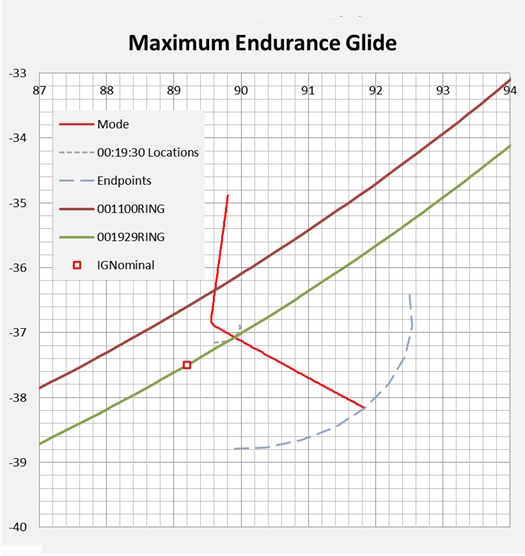
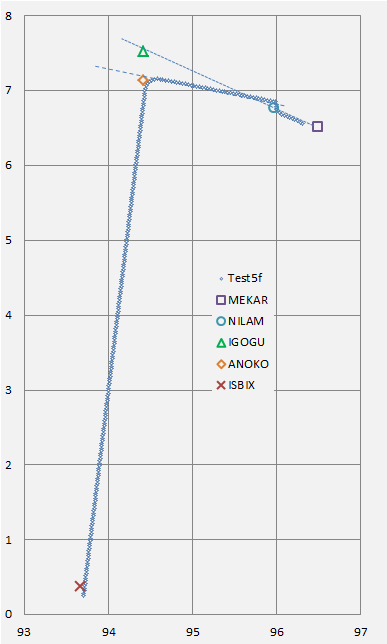
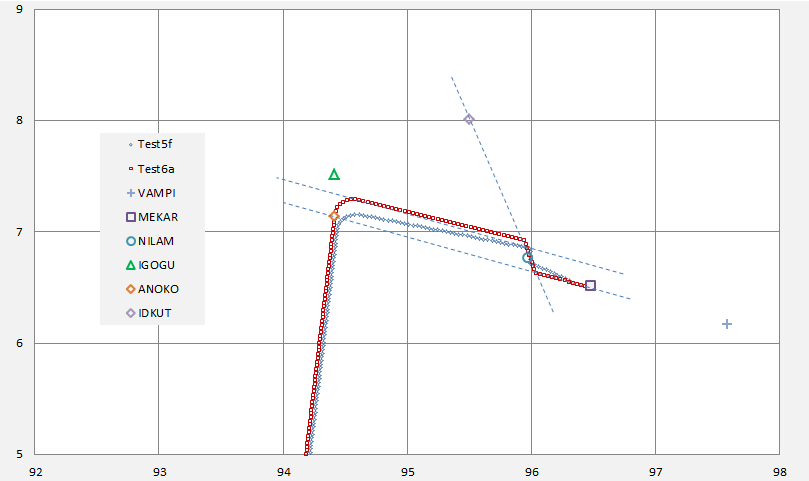
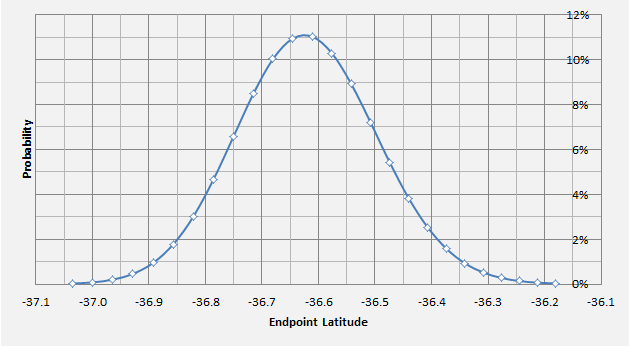
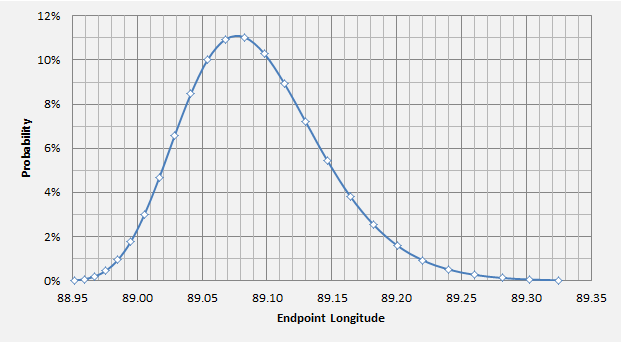
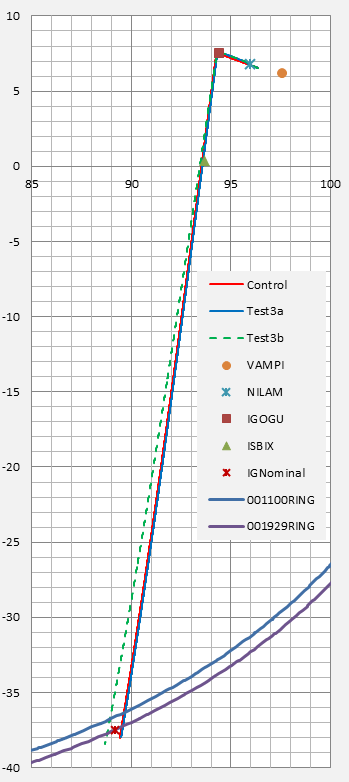
In Figure 2 we give a plan view of the simulated flight paths and the locus of sea level endpoints. The square labelled as IG nominal was reported in [5] as the intersection with the 7th arc, without consideration of a subsequent descent, and is included to assist orientation of this result with respect to previous studies.

Figure 2: Sample Flight Paths and Spread of Probable Endpoints.

In Figure 2 the maximum glide range may be considered as encompassing the region between the lines labelled Mode 1 and Mode 2. The maximum endurance path is shown as a single median line. As the distribution of angles in each case is fairly broad, based on Figure 1, a specific radial vector for the search is not suggested.

 

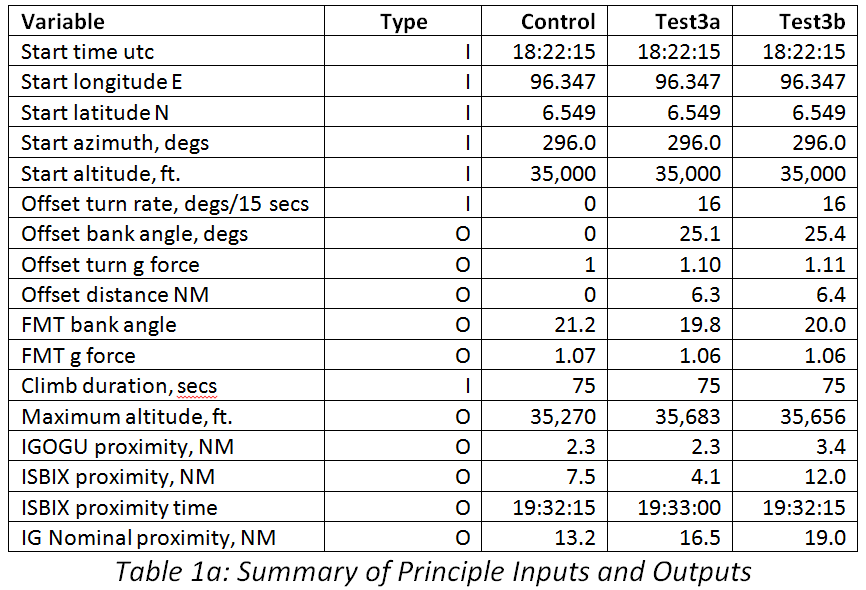
Summary of Model Inputs and Outputs

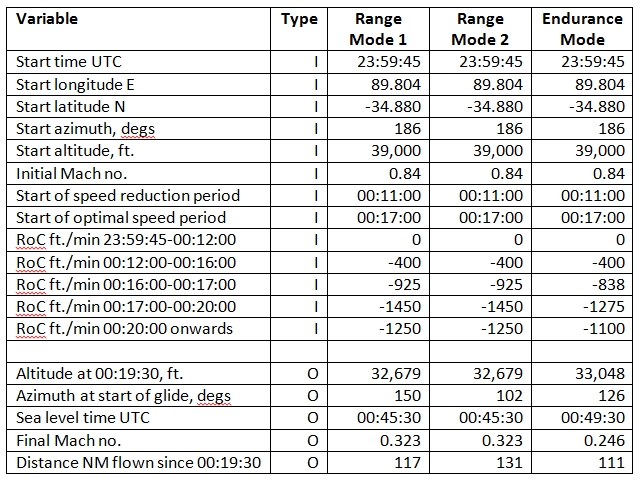
In all scenarios our modelled speeds begin to reduce one minute prior to the commencement of the descent. However, the speed reduction process after fuel exhaustion for the first engine does not have time to reach its optimal OEI speed before fuel exhaustion occurs in the second engine.

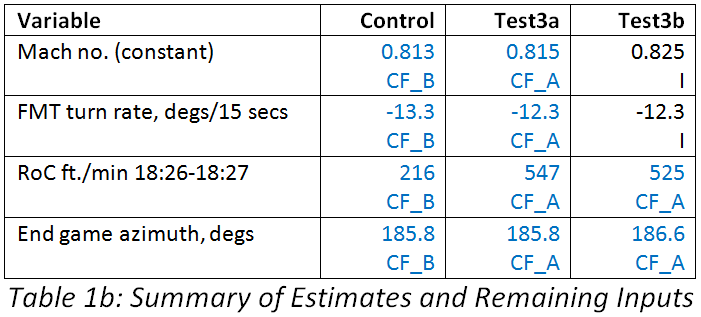
Our model inputs are listed in Table 1 below, along with the consequent outputs.

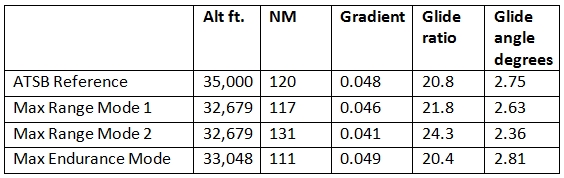
In reference [6] (specifically on page 26) the ATSB estimated a glide range of 120 NM for a descent from 35,000 feet. Our Table 2 below shows a comparison between the glide stages for our sample flight paths and the ATSB’s assumptions. The maximum range Mode 1 scenario covers a similar distance and has a similar gradient to the ATSB’s values.  The differences shown are within the errors of our modelling approximations.

The maximum range scenario for Mode 2 has a larger range and a flatter glide path due to the presence of a tailwind in our simulated flight path. The maximum endurance scenario covers a shorter distance, and but has a similar gradient to that of the ATSB report [6].

 Table 1: Summary of Principal Inputs (I) and Outputs (O). 

 

Table 2: Comparison of Glide Ratios with the ATSB’s Estimates [6]. 

 

Discussion

These scenarios excluded the BFO data at 00:19:29, which has been interpreted to be consistent with a rate of climb (RoC) of about
–4500 feet per minute (i.e. a rapid descent), whereas the RoC for the scenarios studied is about one quarter of this value, as is to be anticipated for a glide. As there are no further usable satellite data for later times, the possibility of a less efficiently flown scenario with a steep initial descent cannot be excluded. This would have the effect of decreasing the range that would be flown after fuel exhaustion (i.e. in the glide phase).

 

Conclusion

We have illustrated two glide range descent scenarios: maximum range and maximum endurance. The conclusions support the ATSB’s findings [6] that MH370 could have flown 120 nautical miles beyond the 7th arc. For pragmatic reasons the ATSB appears to have restricted its search area to a band located 40 nautical miles beyond the 7th arc and parallel to it. However a case is emerging that, if under the control of a pilot, the positions of impact could all lie further still from the 7th arc. Again, on best-available interpretations of the satellite and flight simulator evidence, optimal glide scenarios are not the most likely ones to have occurred, and only represent extreme possibilities. Appropriate risk analyses would be required prior to making proposals for future revisions to search area priorities.

 

Acknowledgments

The authors should like to acknowledge the contribution of Brian Anderson in providing assistance in checking the fuel exhaustion times. We should also like to acknowledge the contributions of Mike Exner, Victor Iannello, and other members of the Independent Group (IG) for their comments on an earlier draft. Any errors or omissions remain the responsibility of the authors.

 

References

[1] Bennett, S., Hyman, G. & Martin, B. (May 2015). MH370 Path Investigation Studies: The Implications of BFO and BTO  Data at 18:27 UTC. Independent Group; available from: https://www.duncansteel.com/archives/1699

[2] Anderson, B. & Exner, M. (March 2015). The Last 15 minutes of Flight of MH370. Independent Group; available from: https://www.duncansteel.com/archives/1461

[3] Ashton, C., Bruce, A. S., Colledge, G. & Dickinson, M. (2014). The Search for MH370. The Journal of Navigation, 68 (01), 1–22. Available from: http://dx.doi.org/10.1017/S037346331400068X

[4] (U.S.) National Centers for Environmental Prediction/National Weather Service/NOAA/Department of Commerce, NCEP FNL Operational Model Global Tropospheric Analyses (continuing from July 1999): Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, Boulder, Colorado. (Updated daily.)

[5] Steel, D. (ed.) (September 2014). MH370 Search Area Recommendation. Independent Group; available from: https://www.duncansteel.com/archives/1023

[6] ATSB: MH370 – Definition of Underwater Search Areas.  External Aviation Investigation AE-2014-054 (26 June 2014; updated 18 August 2014); available from: ATSB: MH370 – Definition of Underwater Search Areas 

[7] Vinh, Nguyen X. (1993). Flight Mechanics of High-Performance Aircraft. Cambridge Aerospace Series. Cambridge: Cambridge University Press.

[8] Pereira, R. L. (2010). Validation of Software for the Calculation of Aerodynamic Coefficients. Degree project, Linkȍping University, Sweden; available from:
http://www.diva-portal.org/smash/get/diva2:329418/fulltext01.pdf 

[9] Jenkinson, L., Simpkin, P. & Rhodes, D. (2001). Civil Jet Aircraft Design. [Data sets] Butterworth-Heinemann; available from: http://booksite.elsevier.com/9780340741528/appendices/default.htm  (accessed 5th June 2015).

[10] Malaysian Ministry of Transport (2015). Safety Investigation for MH370: Factual Information, issued 08 March 2015; updated 15 April 2015; available from: http://mh370.mot.gov.my/

 

Annex A. True Airspeeds and Decent Rates for
Best Range and Endurance

The drag force is assumed to be given by an equation of the form:

…where V is the true airspeed, and z is the altitude. The coefficients are given by:

…where ρ(z) denotes the (ISA) density of air at altitude z and the remaining parameters are as in Table A.1 below.

Table A.1: Parameters Pertaining to the Drag Force

Drag coefficients K and C_d0, reported in [8] and reproduced here in Table A.1., are for the Boeing 777-300 model without operating powerplants, at Mach 0.84 and a Reynolds number of 8.7 × 10^5.

 

Maximum Range Descent

The airspeed which maximises range, in the absence of winds, is given by:

In the absence of engines the steady-state rate of  descent, which maximises range, is [7]:

…where W=mg is the aeroplane weight, and

…is the minimum drag. The glide angle γ_md for this maximum range steady descent is then given by:

 

Maximum Endurance Descent

For maximum endurance (i.e. longest descent time) we can write the following relations (see reference [7]) so as to get the equivalent output parameters as in equations A4, A5 and A6 above:

 

Middle game uncertainties in azimuth, with
implications for the MH370 endpoint

Geoff Hyman
2015 May 11
(May 15: Note correction made in the Conclusions section)
(Document prepared April 2015)

(This report should be read in conjunction with that entitled MH370 Flight Simulation of Path Offset Scenarios.)

Introduction and summary

This investigation was conducted using model BSMv7-10-0 (please see also the first paragraph in this post). To examine some of the scenarios this needed to be modified to allow for a start time and location at the last radar observation.

It is recognised that a short dogleg might have occurred at NILAM and this has been allowed for in the modelling.

The first possibility to be examined is a change in the azimuth after this event, when compared with a pre-set azimuth of 296 degrees true before it occurred.

The next possibility investigated was that a parallel shift occurred. This requires consideration of the uncertainty in the pre-set azimuth.

Azimuth estimation, at different flight phases, used the method of error cost minimisation, which also provided measures of azimuth uncertainty.

Finally, the implications for the uncertainty in the endpoint are examined and brief conclusions are drawn.

Was the azimuth changed at NILAM? (Test 5f) 

At NILAM, was the next waypoint  switched from IGOGU to ANOKO?

Probability of anticlockwise azimuth change at the NILAM dogleg. (Test 5f):

…Or was there a Parallel Shift?  (Test 6a versus Test 5f) 

 

Questions arising:
Was NILAM a temporary route discontinuity?
Was the initial track towards ANOKO?
Did the dogleg head towards IDKUT?
Was ISBIX  the next waypoint?

Comparison of test fits to observations

The improved fit of Test 6a lends support to the idea of a parallel shift (as discussed in more detail here).

What was the Parallel Azimuth? (Test 6a)

Above: probability density for the azimuth before and after the NILAM dogleg. (All other factors remaining constant.)

Mean azimuth = 286.8 degrees;  standard deviation = 3.6 degrees.

Ground Speed and Climb Rates (Test 6a) 

The model uses a constant Mach number, optimised at 0.835. The resulting airspeed at the initial altitude of 39,000 ft was 481 knots.

A wind field was used to convert this to a ground speed. The initial climb rates were estimated by error cost minimisation.

Latitude uncertainty at 00:11 resulting from the middle game azimuth uncertainty (Test 6a) 

Above: probability density for the latitude at 00:11 resulting from the uncertainty in the middle game azimuth. (All other factors remaining constant.)

Mean latitude = -36.6 degrees;
standard deviation = 0.124 degrees (= 7.1 NM)

Longitude uncertainty at 00:11 resulting from the middle game azimuth uncertainty (Test 6a) 

Above: probability density for the longitude at 00:11 resulting from the uncertainty in the middle game azimuth. (All other factors remaining constant.)

Mean longitude = 89.1 degrees;
standard deviation = 0.053 degrees (=2.5 NM)

The longitude distance uncertainty  is scaled by the cosine of the latitude.

Conclusions

• On the basis of the limited evidence used here, the azimuth in the late middle game appears to be fairly uncertain, as is the path navigation mode.
• The magnitude of the parallel shift is substantially reduced after the final major turn.
• The impact of middle game azimuth uncertainty on the uncertainty of the endpoint location appears to be very small.
• Latitude uncertainties are found to exceed longitudinal uncertainties. (Thanks to Brock McEwen for pointing out that this was misstated in the original post here.)
• The topics examined illustrate the continuing interest in questions concerning the role of human factors in flight path determination.

MH370 Flight Simulation of
Path Offset Scenarios  

Geoff Hyman
2015 May 10
Updated May 12

1.  Background and Summary

This note seeks to contribute to a continuing investigation (references [1], [2], [3]) of scenarios describing the period between last radar contact of MH370 and its final descent. The simulations were conducted using variant BSMv7-10-5_GH of a flight model by Barry Martin which may be downloaded by clicking here or here (warning: the download is 20.9 MB; for further information on Barry Martin’s MH370 flight models, see this webpage and this post and also this post and indeed this post too).

The scope of the model employed is sufficient to include a path offset near NILAM, associated with an increase in altitude, as well the final major turn (FMT). All turns are specified in terms of circular arcs with constant rates of turn. The increase in altitude is specified to be at a constant rate of climb (RoC). The program supports a temporal resolution of 15 seconds, proximity calculations of flight paths from designated waypoints, outputs relating to turn characteristics, plus a range of error criteria which may be used either to compare the statistical fit of alternative flightpath or to estimate selected unknown flight parameters.

The principal finding from the current investigation is that the most probable scenario is an offset path during the late middle game which did not continue beyond the FMT. Implications in terms of human and system factors are discussed.

The implied zero altitude locations from all of the tests are close to the published nominal IG September 2014 location [4], given as 37.5S, 89.2E. This report does not deal with estimated endpoint coordinates, as this requires a more detailed simulation of the final descent [5].

 

2.  Initial Conditions, Key Outputs and Estimates

Table 1a shows the major input assumptions and principal model outputs. The second column in Table 1a, labelled ‘type’, adopts the abbreviations:
I:          Input values/initial conditions
O:        Values computed explicitly from the flightpath model

For some of the variables, values were estimated by minimisation of an error cost function (CF), using an approach which varied between the modelled scenarios, as specified in Table 1b.

The value of the error cost function depends on both the underlying uncertainty in their true values and on which observations are selected for error cost minimisation. Further details of the specification of the error cost function are given in Annex 1 and in Section 4 below.

For the scenarios reported here, the start azimuth was assumed to be at the N571 alignment of 296 degrees (measured through east from true north). To conform to limits of lateral navigation, all turns were constrained to be within a bank angle that did not exceed approximately 25 degrees. The corresponding g force experienced would therefore not exceed 10% above normal gravity. The equations used for the banked turn calculations are given in Annex 2. The FMT was constrained to terminate by 18:40 and to be executed within a period of just over two minutes.

Each scenario used a different approach to select which of the unknowns were estimated, and which observations were used to estimate them.  In Table 1b, CM_A and CM_B refer to different subsets of observations employed for cost minimisation, as detailed in Table 2.

It can be noted that the estimated Mach numbers were similar in the Control scenario and Test 3a. For Test 3b a slightly higher value was input, to produce an offset which continues into the end-game (i.e. post-FMT). The estimated climb rates (RoC) were moderate but varied between scenarios, giving increases in altitude of over 500 feet for Tests 3a and 3b, but of less than 220 feet for the Control scenario.

The proximity (minimum distance) from the nominal IG September 2014 location were all computed assuming an altitude of zero (i.e. assuming that the 7th ping ring is located close to, or at, sea level; see this recent post). However, the waypoint and offset distances were calculated by finding the minimum distances of the offset paths from a reference location on the Control path, at a common altitude of 35,000 feet.

 

3.  Three Scenarios, a Suggested Interpretation and a Disclaimer

The selection of the three scenarios presented arose from a suggestion made by Sid Bennett, who set out clearly how they might be expected to operate. His contribution is gratefully acknowledged. Their suggested interpretation arises from discussions with Barry Martin, who created the program being used for flight path analysis and whose contribution is also gratefully acknowledged. Any errors or misunderstanding in this report are entirely my own. Two short extracts from Sid’s proposals are given in italics below.

The Control scenario represents a flight path with no offset. Its statistical support requires setting aside the 175 Hz BFO observation at 18:27. This type of scenario may have been implicit when the IG presented its September 2014 report.

Test 3a assumes that the 18:27 BFO observation is valid and results in an offset path, commencing shortly after the NILAM waypoint. This is an example of the type of scenario which was examined in [2] and in recent discussions within the IG. It transpires that, under the specified modelling assumptions for this test, the calculated path offset was not maintained after the IGOGU waypoint (i.e. there was ‘offset cancellation’). It seems that such a scenario is unlikely to be a result of the automatic operation of the flight management system (FMS), which would require the final major turn to exceed 135 degrees. Instead it would appear to require active human intervention near IGOGU:

“… the pilot cancels the offset either sometime before IGOGU or sometime after IGOGU, but before ISBIX. In the end, both options result in the plane flying the radial between IGOGU and ISBIX…” (Sid Bennett)

This may be contrasted with Test 3b, a path for which the path offset is maintained beyond the FMT:

“… After continuing the offset track south of IGOGU, the track continues parallel to the radial joining IGOGU and ISBIX as a geodesic until abreast of ISBIX and then continues as a lox [loxodrome] without changing the azimuth…” (Sid Bennett)

This scenario could, in theory, have been flown by the FMS, so it would not have required human intervention.

The formulation of these alternatives is particularly interesting. Assuming that they characterise the possibilities we might proceed by a process of elimination. First, if we were convinced that an offset had occurred, this would eliminate the Control scenario. The initial offset would have required active human intervention at about 18:27.  If it were impossible in practice for the satellite data to discriminate between offset continuation and offset cancellation, it would then be difficult to determine if human intervention had or had not continued. Alternatively if one or other of the offset scenarios (Test 3a, Test 3b) could be eliminated then this ambiguity would be resolved. The following interpretations of the scenarios are proposed:

We will assess the comparative weight of evidence in favour of each of these cases.

 

4.  Specification of the Cost Functions in terms of their constituent observations

Table 2 reports the BFO and BTO observations which were used in each of the error cost functions. The grey cells indicate observations which were excluded from individual cost functions. The black cells show where no BTO observations were available.

For CF_A the BFO observation at 23:14:00 was excluded. This cost function was used to estimate unknowns in Tests 3a and 3b. For CF_B the observations (both BFO and BTO) at 18:25:30 and at 18:27:00 were excluded. This was used for the estimation of unknowns in the control scenario. The program automatically excludes all observations which occurred prior to the common start time of the scenarios of 18:22:15.

 

5.  The Appearances of the Flight Paths for the Three Scenarios

Figure 1 shows the three flight paths over the full simulation period. At this resolution two paths (the red path is for the Control scenario, and blue path for Test3a) appear indistinguishable. They both pass within 20 nautical miles (NM) to the east of the nominal IG September 2014 location (37.5S, 89.2E; shown by the red X marker on the 7th ping ring). The dashed green Test 3b path passes within 20 NM to the west of the nominal IG September 2014 location.

Figure 1: The Three Flightpaths in relation to the
Nominal IG September 2014 location

Figure 2 shows the paths in the vicinity of the ISBIX waypoint. The closest proximity between the Test 3a path and ISBIX is 4 NM, while the closest proximity of the Test 3b path to ISBIX is 12 NM, a difference of 8 NM.

Figure 2: The Three Flightpaths in relation to the ISBIX waypoint

If we refer back to Table 1a we may note that the middle-game offset distance for both of these paths is between 6 and 7 NM. The difference of 8 NM distance from ISBIX  is therefore sufficient to discriminate between a flightpath for which the offset is cancelled and one for which it is maintained.

The intersection of the Test3b path and the Control path, at a latitude near 5.7 degrees north, is also apparent in Figure 2.

In Figure 3, the red Control path exhibits no offset. Test 3a and 3b (dashed) have offsets starting near the NILAM waypoint, at distances of slightly over 6 NM from the Control path.

The early end-game path for the Control scenario commences to the west of the Test 3a path. This is unsurprising because, during the late middle-game, the offset paths are longer than the Control path. The Control path has the same speed as Test 3a, so it can proceed further west in the same elapsed time as the Test 3a path. The same check could not be used to compare the Control path with Test 3b, as the latter has a slightly higher speed.

Figure 3: The Three Flight Paths in relation to
NILAM, IGOGU and the Final Major Turn 

6.  Error Analysis

Table 3 shows the BFO and BTO errors for each of the three scenarios. Values in excess of three standard deviations have been highlighted in yellow. Two of these errors apply to all three scenarios: the BFO errors at 18:25:30 and 23:14:00. At 23:14 similar errors have been noted for examined previously scenarios [2] and these could be either intrinsic to the observations, or due to unknown factors which have not been accommodated in any of the modelled scenarios. Previous simulations support the view that the 18:25:30 errors are correlated with the value of the middle-game azimuth.

Next we look at those errors which help us discriminate between the current scenarios (Control, Test 3a, Test 3b). By far the largest error is for the BFO observation of 175 Hz at 18:27 when compared with the Control scenario. The best available explanation that we currently have for this is that an offset turn had occurred. This error is not present in the other two scenarios. Comparing Test 3a with Test 3b we note that the latter has two large BTO errors: at 19:41 and 22:41:15. For Test 3a, while errors are also present at these times they are of a much smaller magnitude. A broader statistical assessment is of interest.

Table 4 below reports the values of the error cost functions and their BFO and BTO constituents.

The second column in Table 4 indicates the cost function being reported, with an asterisk (*) being used to indicate which of them was used to estimate the unknowns. Test 3a performed best for both cost functions, and also for their BFO and BTO components.

The worst values are highlighted in yellow. The Control scenario performed the worst for CF_A, while Test 3b performed the worst for CF_B.

Pairs of scenarios can be compared by treating the error costs as standard normal deviates and calculating odds ratios. On this basis under cost function A (CF_A), Test 3a would have ten times higher a likelihood than Test 3b; and under cost function B (CF_B), Test 3a would have twenty times the likelihood. From either view, it would be reasonable to reject Test 3b (the continuing offset scenario). It remains a challenge to construct continuing offset scenarios which achieve substantially better performance with respect to the same observations.

The comparative odds for each of the test paths (3a, 3b) can also be compared with the Control scenario. Clearly under CF_A the Control scenario would be very strongly rejected, so it suffices to restrict attention to CF_B. On this basis the offset cancellation scenario (Test 3a) is only twice as likely as the Control scenario. Therefore, if the null hypothesis was the Control (no offset) scenario, it could not be rejected with a high degree of confidence.

We appear to be faced with a realistic choice only between either the no offset scenario (the Control scenario) or the offset cancellation scenario (Test 3a). Which of them is correct depends on the validity of the observations near 18:27 UTC. If they are considered valid then we have eliminated everything but the offset cancellation scenario.

 

7.  Implications of Findings for Likely Scenarios and Human versus System Factors 

In discussing the full set of findings we needed to discuss alternative stances with respect to the satellite observations at 18:27 (cf. the apparently-large BFO at that time). First, we will adopt a sceptical view and exclude them from consideration.  A scenario without an offset is simpler as it has fewer degrees of freedom. An application of Occam’s razor would thereby make the no offset (Control) scenario the null hypothesis. On the sceptical view, this could not be rejected with a reasonable degree of confidence and the case for an offset would be weak, even though it appears as a slightly more likely alternative. Without an offset no human intervention would be implied during the late middle-game, and again this would seem to be a simpler interpretation of events. However its simplicity also makes it easier to falsify.

Next, we include the 18:27 observations, accepting them as valid. The case for an offset now becomes extremely strong and the issue is primarily whether or not it was cancelled. The scenarios presented here support the view that offset cancellation is the more likely scenario. The implication would be that human intervention had probably occurred, and that it had continued at least until the vicinity of IGOGU.

Conclusions concerning the continuation of human intervention beyond ISBIX, until the final descent, are outside the scope of this report.

  

References

[1] Bennett S. and Hyman G. Further Studies on the Path of MH370: Turn Time and Final Azimuth. MH370 Independent Group, March 2015.

[2] Hyman G., Middle game uncertainties in azimuth, with implications for the MH370 endpoint. MH370 Independent Group, April/May 2015.

[3] Exner M., Godfrey R. and Bennett S. The Timing of the MH370 Final Major Turn.  Independent Group, March 2015.

[4] Steel D., MH370 Search Area Recommendation. MH370 Independent Group, September  2014

[5] Anderson B. The Last 15 minutes of Flight of MH370. MH370 Independent Group, April 2015.