Middle game uncertainties in azimuth, with
implications for the MH370 endpoint

Geoff Hyman
2015 May 11
(May 15: Note correction made in the Conclusions section)
(Document prepared April 2015)

(This report should be read in conjunction with that entitled MH370 Flight Simulation of Path Offset Scenarios.)

Introduction and summary

This investigation was conducted using model BSMv7-10-0 (please see also the first paragraph in this post). To examine some of the scenarios this needed to be modified to allow for a start time and location at the last radar observation.

It is recognised that a short dogleg might have occurred at NILAM and this has been allowed for in the modelling.

The first possibility to be examined is a change in the azimuth after this event, when compared with a pre-set azimuth of 296 degrees true before it occurred.

The next possibility investigated was that a parallel shift occurred. This requires consideration of the uncertainty in the pre-set azimuth.

Azimuth estimation, at different flight phases, used the method of error cost minimisation, which also provided measures of azimuth uncertainty.

Finally, the implications for the uncertainty in the endpoint are examined and brief conclusions are drawn.

Was the azimuth changed at NILAM? (Test 5f) 

At NILAM, was the next waypoint  switched from IGOGU to ANOKO?

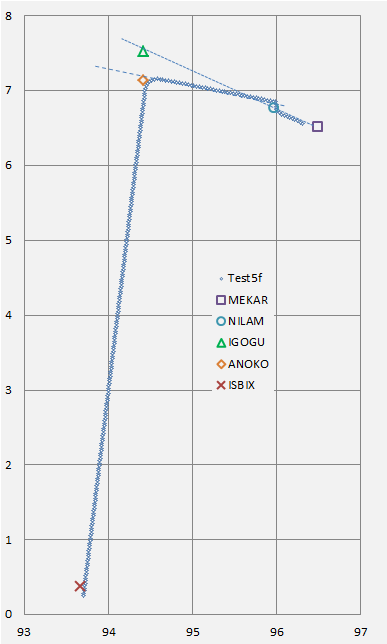
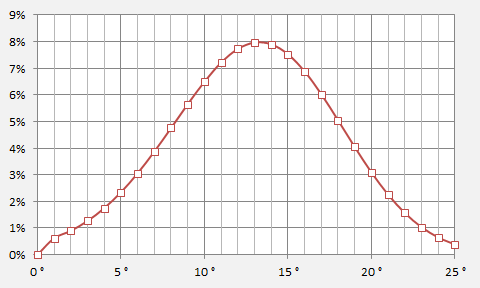
Probability of anticlockwise azimuth change at the NILAM dogleg. (Test 5f):

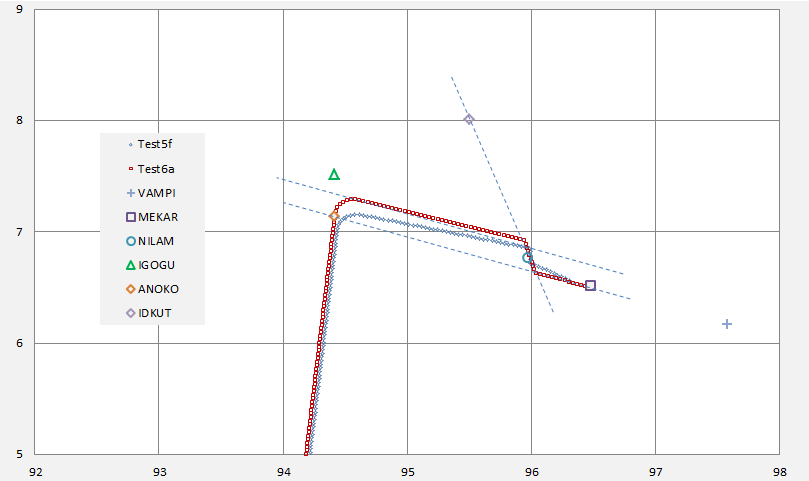
…Or was there a Parallel Shift?  (Test 6a versus Test 5f) 

 

Questions arising:
Was NILAM a temporary route discontinuity?
Was the initial track towards ANOKO?
Did the dogleg head towards IDKUT?
Was ISBIX  the next waypoint?

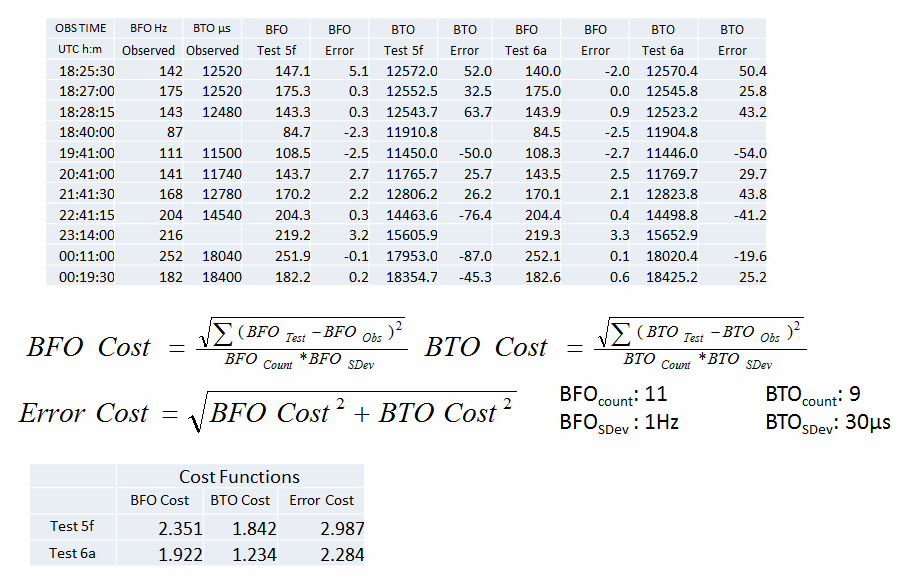
Comparison of test fits to observations

The improved fit of Test 6a lends support to the idea of a parallel shift (as discussed in more detail here).

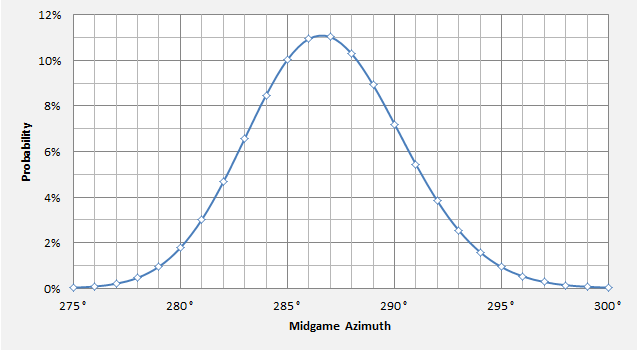
What was the Parallel Azimuth? (Test 6a)

Above: probability density for the azimuth before and after the NILAM dogleg. (All other factors remaining constant.)

Mean azimuth = 286.8 degrees;  standard deviation = 3.6 degrees.

Ground Speed and Climb Rates (Test 6a) 

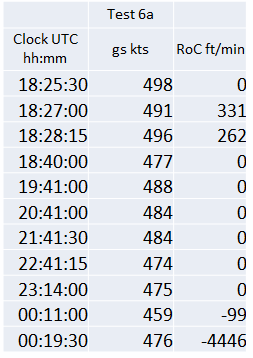
The model uses a constant Mach number, optimised at 0.835. The resulting airspeed at the initial altitude of 39,000 ft was 481 knots.

A wind field was used to convert this to a ground speed. The initial climb rates were estimated by error cost minimisation.

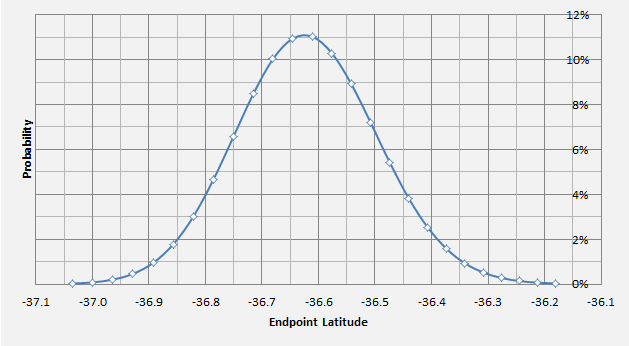
Latitude uncertainty at 00:11 resulting from the middle game azimuth uncertainty (Test 6a) 

Above: probability density for the latitude at 00:11 resulting from the uncertainty in the middle game azimuth. (All other factors remaining constant.)

Mean latitude = -36.6 degrees;
standard deviation = 0.124 degrees (= 7.1 NM)

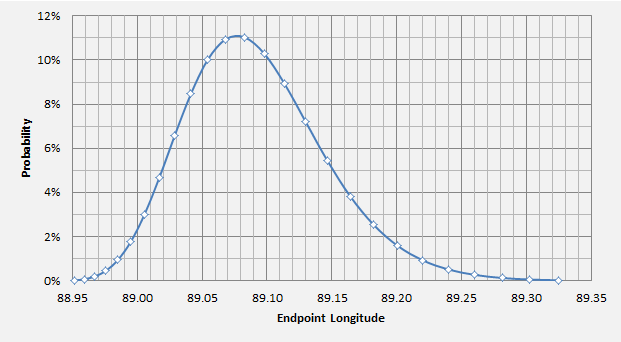
Longitude uncertainty at 00:11 resulting from the middle game azimuth uncertainty (Test 6a) 

Above: probability density for the longitude at 00:11 resulting from the uncertainty in the middle game azimuth. (All other factors remaining constant.)

Mean longitude = 89.1 degrees;
standard deviation = 0.053 degrees (=2.5 NM)

The longitude distance uncertainty  is scaled by the cosine of the latitude.

Conclusions

• On the basis of the limited evidence used here, the azimuth in the late middle game appears to be fairly uncertain, as is the path navigation mode.
• The magnitude of the parallel shift is substantially reduced after the final major turn.
• The impact of middle game azimuth uncertainty on the uncertainty of the endpoint location appears to be very small.
• Latitude uncertainties are found to exceed longitudinal uncertainties. (Thanks to Brock McEwen for pointing out that this was misstated in the original post here.)
• The topics examined illustrate the continuing interest in questions concerning the role of human factors in flight path determination.